Rigid and Flexible Pipes
Buried pipelines for the conveyance of potable water and sanitary sewers form the bedrock of our civilization. The very basic services that we take for granted, such as a running faucet with clean drinking water and the ability of our wastewater to be transported away from our homes and businesses for treatment and release into the environment, are possible because of the vast network of buried pipes that lie hidden beneath roads and the concrete jungles that define the large urban centers that are our cities.
These intricate networks consist of various types of pipe materials that range from metals to concrete to plastics to composites. Whatever the material type, all are expected to provide some minimum service qualities: prevention of leaks, which ensure that potable water isn’t compromised by contaminants entering a piping system and that wastewaters do not pollute soils and existing sources of groundwater, and most importantly, that the structural soundness of a buried pipe system results in a minimum service life of 50 to 100 years. The latter can only be ensured through a thorough understanding of and designing for the loads to which a buried pipe will be exposed, its response to the loading, and the interaction mechanism between the pipe and surrounding soils.
While an understanding of pipe-soil interaction is important for the sound structural design of pipelines, it should be noted that the concern for soil pressure on a pipe is limited to empty pipe or gravity flow pipelines where the conduit never flows full. In municipal pressure piping systems, the internal pressure is typically much greater than soil pressure on the pipe; internal pressure essentially supports the soil load when the line is placed into service.
The story of the formal study of buried pipe structures in North America begins in Ames, Iowa, at the turn of the 20th Century, when Dr. Anson Marston, then Dean of Engineering at the Iowa State College (now Iowa State University) and the first Chairman of the Iowa State Highway Commission, analyzed soil pressures on buried culverts in an effort to drain muddy rural roads. Research was also necessary as thousands of small wooden bridges were being replaced by concrete and clay pipes placed in stream beds underneath roadway embankments. It was necessary to design them properly so that they would not fail.
Buried pipe design, then, was inextricably connected to the development of highway systems in the United States. Marston was the first Chairman of the federal Highway Research Board. Our knowledge of pipe-soil interaction, as well as the development of new pipe materials and the improvement of traditional ones, has grown by leaps and bounds since those early days, leading to a multi-billion dollar global pipe materials industry. Another relatively new construction method in buried pipeline construction and rehabilitation is the advent of trenchless technology.
While trenchless technology is no longer in its infancy, the only known and practiced trenchless construction methods during Marston’s lifetime included jacking and tunneling, and little else. But a tremendous amount of research in the last two decades now provides design engineers and contractors with an understanding of the pipe-soil mechanics of pipelines built by methods other than traditional open-trench methods.
Classical Pipe-Soil Interaction Theory
In 1913, and 1930, Marston published his original papers “The Theory of Loads on Pipes in Ditches and Tests of Cement and Clay Drain Tile and Sewer Pipe” and “The Theory of External Loads on Closed Conduits in the Light of the Latest Experiments,” respectively, marking the earliest systematic approach of studying the structural mechanics of buried pipes. Thus was defined the Marston Theory of Loads on buried conduits.
This became, in part, the very foundation on which much of the later work around the world on earth loading technology of buried pipes was based. In 1941, Marston’s student Merlin Spangler, known today as “the father of buried flexible pipe design,” published another ground-breaking paper, “The Structural Design of Flexible Pipe Culverts,” in which he derived an equation, the Iowa Formula, for predicting the ring deflection of buried flexible pipes. Spangler would later become chairman of the Culvert Committee of the federal Transportation Research Board. In 1958, Spangler’s student, Reynold Watkins, published “Some Characteristics of the Modulus of Passive Resistance of Soil – A study in Similitude,” in which he solved a fundamental flaw in the dimensions of a modulus of passive resistance in Spangler’s Iowa Formula, defining a new modulus of horizontal soil reaction, E’, in the Modified Iowa Equation. In later years, other significant contributions came from A. Howard, J. Duncan, J. Hartley, F. Heger, T. McGrath, M. Zarghamee, and others that now enable the external load design of rigid and flexible pipes to be an even more exact science.
The Marston Load Theory

The basic concept of the Marston Load Theory is that the load on a buried pipe, because of the weight of the column of soil, or central prism, directly above the pipe, is modified by the response of the pipe and the relative movement of the side columns of soil, or external prisms (adjacent to the pipe, between the pipe and the trench walls on either side), to the central prism. The relative movement of the central prism and the side prisms result in shearing stresses or frictional forces, calculated using Rankine’s theory.
Rigid Pipe
Marston recognized that in a trench (generally, trench width = 2 x pipe diameter), when the side columns of soil or the external prisms are more compressible than the pipe due to its inherent rigidity, this causes the pipe to assume load generated across the width of the trench. The shearing stresses or friction forces that develop due to the differential settlement of the external prisms and the central prism are additive to the load of the central prism alone. Pipes that behave in this manner are referred to as Rigid Pipes. Generally, rigid pipes start showing signs of structural distress before being vertically deflected 2 percent. Rigid pipes include reinforced non-cylinder concrete, reinforced concrete cylinder, prestressed concrete cylinder, vitrified clay, polymer concrete, cast iron, asbestos cement and cast-in-place pipes.
Flexible Pipe
On the other hand, if a pipe is more compressible than the external soil columns, without any structural damage caused to the pipe as a result of its vertical deflection, allowing the central prism to settle more in relation to the external prisms, the actual load on the pipe is less than the load of the central prism due to the direction in which the shearing stresses or friction forces develop as a result of the differential settlement of the central prism in relation to the external prisms. Pipes that display this behavior when buried are referred to as Flexible Pipes. Use of the prism load is conservative because installers do not compact soil against the pipe. The pipe is embedded in a “packing” of less dense soil that serves the same way as does packing around an item in a shipping container. The pipe is relieved of part of the prism load which the soil then picks up in arching action over the pipe.
As a general rule, flexible pipes will deflect at least 2 percent without structural distress. Most flexible pipe material standards allow up to 5 percent deflection. Deflection is limited to 2 percent if the flexible pipe has a rigid lining and coating and 3 percent for a rigid lining and flexible coating. Flexible pipes include steel, ductile iron, thermoplastics such as Polyvinyl Chloride (PVC) and High Density Polyethylene (HDPE), thermosetting plastics such as fiberglass-reinforced polymer (FRP), bar-wrapped concrete cylinder pipe, and corrugated steel pipes.
Semi-Rigid Pipe
Some pipe materials exhibit characteristics of both rigid and flexible pipes, primarily controlled by their diameters, and are referred to as semi-rigid. Attempts have been made to define semi-rigid pipes as those that will deflect between 0.1 percent and 3.0 percent without causing harmful or potentially harmful cracks. Bar-wrapped concrete cylinder pipe is an example. But since current design standards are based on the concept of a rigid or a flexible pipe, the term carries only marketing value and little else. Like all flexible buried pipes, bar-wrapped concrete cylinder pipe design is also subject to a deflection limit, thus making it a flexible pipe.
Pipe-Soil Interaction in Embankment Conditions
A positive embankment installation condition, where the pipe is installed underneath an embankment, in shallow bedding, with its top projecting above the surface of the natural ground, is another commonly-encountered scenario for buried pipe design and installation. The loads and shearing forces just discussed for trench conditions also play a key role in embankment conditions. As indicated in figure 3a and 3b, the imaginary vertical planes extending upward from the sides of a buried pipe are the planes along which relative movements are assumed to occur and on which shearing forces are generated.
pBc is the vertical distance from the natural ground surface to the top of the structure, where p is the projection ratio, the vertical distance between the top of the pipe and the ground or bedding surface divided by the diameter of the pipe, Bc. sm is the compression strain of the side columns of soil of height pBc, sg is the settlement of the natural ground surface adjacent to the pipe, sf is the settlement of the pipe into its foundation, and dc is the shortening of the vertical height of the conduit. A settlement ratio, rsd, is then defined using the formula:

Since it was almost impossible to predetermine the settlement ratio that would develop in a specific case, Marston tabulated it as an empirical quantity, based on the type of pipe material (rigid or flexible), and foundation conditions for rigid pipe and side-fill soil condition for flexible pipe.
The critical plane is the horizontal plane through the top of the pipe when the fill is level with its top. At critical plane, H=0. During and after construction, if this critical plane settles more than the top of the pipe, as shown for rigid pipe in figure 3a, the settlement ratio is positive (prsd>0). For flexible pipes, figure 3b, the critical plane settles less than the top of the pipe, indicating the settlement ratio is negative (prsd<0).
For positive projecting conduits, Marston also determined, initially purely through mathematical reasoning, the existence of a horizontal plane above the pipe where shearing forces would be zero, referred to as the plane of equal settlement. Settlement of interior and exterior prisms above this plane is equal.
Marston Load Calculations in Trench Condition
For pipe installed in a trench, Marston defined the soil load on a rigid pipe as:
where, Wc is the load on the pipe in trench Cd is a dimensionless load coefficient for trench condition that accounts for the ratio of the height of fill to width of the trench, and the shearing forces between interior and adjacent soil prisms w is the unit weight of soil, and Bd is the trench width
For flexible pipe, with side fills having essentially the same degree of stiffness as the pipe itself (note that this condition is essential to use Equation 3), he derived the following equation:
where, Bc represents the outside diameter of the pipe
As can be seen from Equations 2 and 3, the width of a trench directly affects the loads imposed on both rigid and flexible pipes. In the case of a flexible pipe, where the pipe stiffness and side fill stiffness are essentially equal, however, the diameter of the pipe also affects the magnitude of the load. For identical conditions of installation, then, the ratio of the load on a flexible pipe to the load on a rigid pipe is equal to the ratio of the pipe diameter to the width of the trench.

If the trench is twice as wide as the buried pipe, the load imposed on a rigid pipe will be twice the load imposed on a flexible pipe with side fills having the same degree of stiffness as the flexible pipe itself.
Load Calculations in Embankment Condition
For pipe installed under an embankment, Marston derived another formula, equation 4.

where Wc is the load on the pipe under embankment Cc is a dimensionless load coefficient for embankment condition that accounts for the ratio of the height of fill to pipe diameter, the shearing forces between interior and adjacent soil prisms, and the direction and amount of relative settlement between interior and adjacent soil prisms w is the unit weight of soil, and Bc is the pipe diameter
Since there is no trench by definition of a positive embankment condition, the trench width, Bd, is not a part of equation 4. For Cc, when the product of the settlement ratio, rsd, and the projection ratio, p, equals zero, i.e. prsd = 0, then Cc = H/Bc. If this is substituted into Equation 4, the load on a pipe underneath an embankment is defined as
where, H is the burial depth of the pipe
Equation 5 is referred to as the prism load. As stated earlier, for rigid pipes, settlement ratio under an embankment is positive (prsd>0) and for flexible pipes, settlement ratio is negative (prsd<0). The condition prsd = 0 for flexible pipe is therefore conservative and is the maximum load that will be imposed by soil on a flexible pipe in virtually all cases. In practice, for design purposes, under both trench and embankment conditions, the prism load is always used for flexible pipes.
Pipe in Wide Trenches
Equation 2 for rigid pipes indicates that the load on buried pipe is directly related to the trench width, i.e. the wider the trench, the higher the load. This relationship between trench width and load is applicable and equation 2 for trench condition can be used for all trench widths below that which gives a load equal to the load indicated by equation 4 for a positive embankment condition. The width at which the load equality for the two equations develops is referred to as the transition width. The embankment equation (4) must be used for rigid pipes beyond the transition width.
Corroboration of Marston Load
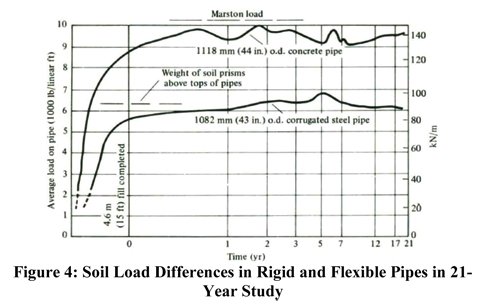
Marston’s observations of load on buried pipe were validated in a 21-year study, from 1927 to 1948, where concrete, cast iron (both rigid pipes) and corrugated steel pipes (flexible pipe) were buried under an embankment of 15 ft. Measured loads on the pipes were compared with loads calculated by the Marston theory of loads on underground conduits, and were found to closely agree. Figure 4 presents measured loads on the concrete and corrugated steel pipe. It can be seen that the load on the concrete pipe was consistently 50 percent greater than that on the corrugated steel pipe of approximately the same diameter.
This load difference can be attributed to the difference in vertical deflection of the pipes that influenced the settlement ratios, and the magnitude of the shear stress components, as correctly theorized by Marston for flexible and rigid pipe materials. His assertion that the load on a rigid pipe would always be higher than the load on a flexible pipe due to the differences in interaction between each type of pipe with surrounding soils was therefore corroborated. The study also verified the presence of a plane of equal settlement which Marston had originally predicted purely based on mathematical reasoning.

Trenchless Technology
In recent years, the challenges of constructing new or rehabilitating old buried pipeline infrastructure in highly developed urban areas has lead to the development of various construction and renewal methods that avoid the cutting of trenches and cause minimal surface intrusion. Generally referred to as trenchless technology, these methods include directional drilling, microtunneling, pipe jacking, auger boring, sliplining, pipe bursting, and others. The load on a jacked or tunneled conduit, can be described as:
where, Wt is the load on a jacked or tunneled pipe Ct is a dimensionless load coefficient for tunneled or jacked pipe w is the unit weight of soil, and Bt is the maximum width of bore excavation c is the cohesion of the soil above the excavation
The vertical load at the top of the bore within the width of the excavation is the upward friction forces and the soil cohesion along the limits of the soil prism directly above the bore subtracted from the weight of the prism above the bore. The 2cCtBt in Equation 6 represents the cohesion of undisturbed soils.
In North America, the field of horizontal directional drilling (HDD) has made significant progress due to extensive research by Tom Iseley, referred by some as “the father of trenchless technology,” Ray Sterling, Larry Petroff, Mohammed Najafi, Samuel Ariaratnum, Larry Slavin, Erez Allouche, Alan Atalah, Ian Moore, Mark Knight and others. HDD is the most widely utilized method of trenchless construction in North America. ASTM F1962, Standard Guide for Use of Maxi-Horizontal Directional Drilling for Placement of Polyethylene Pipe or Conduit Under Obstacles, including River Crossings, provides an understanding of earth loading pressures and subsequent pipe deflection for thermoplastics such as HDPE when installed by HDD.

Soil loading on pipe installed by HDD is dependent on many of the same parameters as pipes installed by open-trench method, such as depth of bury, in-situ soil properties, pipe diameter, etc., but additionally, other factors such as the mud-slurry properties and diameter of boreholes play critical roles also. Since HDD boreholes are typically 50 percent larger than the outside diameter of the pipe, it is the deformation of the soil around the borehole that transfers earth loads (and live loads if applicable) to the pipe itself. According to ASTM F1962, “As the deformation occurs, a cavity of loosened soil forms above the borehole. This cavity is filled by soil sloughing from above it. The process causes the soil to bulk, that is, the density of the sloughed soil is less than the density of the undisturbed soil. The sloughing process continues until an equilibrium is reached where the stiffness of the sloughed soil is sufficient to resist further sloughing from the soil above. This bulking state results in arching of load around the pipe (that is, the earth load applied to the pipe is less than the geostatic stress or prism load).” Figure 5 illustrates this.
Only when a pipe is drilled into a depth that is at least five times the outside diameter of the pipe should credit for arching be considered. While the document acknowledges a lack of published equations for calculating earth loads on pipes installed by HDD, it makes references to some recent publications on soil arching in other trenchless construction methods that may be utilized to arrive at a realistic loading on the pipe. An equation is provided to calculate the possible deflection of the pipe.
Conclusion
In addition to the importance of accounting for the soil load on buried pipe (dead load), it is also important to account for live loads, whenever applicable, such as moving vehicles (live load) when a pipe is buried under a highway or railroad embankment. One way in which this is done is by use of modified Boussinesq equations, details of which were not discussed in this article.
It is important to remember that the concern for soil pressure on a pipe is limited to empty pipe or gravity flow pipelines where the conduit never flows full. In municipal pressure piping systems, where the internal pressure is typically much greater than external soil pressure, the former supports the latter when the line is placed into service. For larger diameter flexible pressure pipelines however, it is always appropriate to run a check that the soil conditions are appropriate to limit the pipe’s allowable vertical deflection as permitted by specification and to prevent any damage to rigid linings and/or coatings due to excessive deflection.
The value of soil load analysis is to arrive at the required pipe strength necessary to build a municipal pipeline of sufficient structural integrity to serve its design life. The design process varies from rigid to flexible pipe, and usually by pipe material also. The second part of this series in the next issue will review current design practices for rigid and flexible pipes with regards to earth loading.
Shah Rahman is the western regional engineer for Northwest Pipe Co., based in Southern Calif. He is an Associate Editor (Pipe Materials) for the ASCE Journal of Pipeline Systems Engineering and Practice.
References




