What Is Viscosity? Part 2
In the October issue, Manley Osbak opened his discussion of viscosity and considered shear stress and shear rate in detail. In this final article of the two-part series, he will explain how shear stress and shear rate are connected to viscosity and define exactly what viscosity is.
The methods that we often use to manage viscosity are justified in part, by our concept of what viscosity is. Generally, we consider viscosity to be another word for thickness. We believe that if a drilling fluid has the right thickness, it must have the right viscosity and if it has the right viscosity, it must have good suspension characteristics and carrying capacity. Since our intuitive understanding allows us to make reasonable assessments of thickness, we believe that we can use that intuitive understand to make reasonable assessments of viscosity, and the resulting suspension and carrying capacity. While viscosity is a way of describing thickness, it is an over-simplification to consider viscosity as the same thing as thickness as we intuitively understand it. The tools and processes that we use to manage viscosity, borne out of our intuitive understanding of thickness, may also be over-simplified, resulting in a management process that fails to effect the full work potential of the fluid.
We have established in our discussion so far (see the October issue of Trenchless Technology) that the water moving through a pipe, splits up into layers, with each layer sliding over top of, and slightly faster than, its outside neighbor. The layer that is touching the wall of the pipe, called the boundary layer, doesn’t move at all; while the layer that is in the centre of the pipe, called the free stream layer, is moving the fastest. The further each layer is from the boundary, the faster it is moving, with each layer increasing in speed by the same amount.
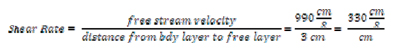
In our pipe example, the water against the wall of the pipe (the boundary layer) would have a velocity of 0 cm/s, and let’s say that the water in the free stream layer has a velocity of 990 cm/s. If the water is split up into 100 layers between the boundary layer and the free stream layer, then each layer would be going 9.9 cm/s faster than its outside neighbor. The important point here is that the incremental increase in speed is the same from layer to layer as we move from the boundary layer to the free stream layer.
The speed of each layer of water not only increases by the same amount from layer to layer, but it also increases by the same amount from centimeter to centimeter. The difference in velocity, or the velocity differential, between the boundary layer and the free-stream layer is 990 cm/s in our example. If the pipe has an internal diameter of 6 cm, then the distance between the boundary layer and the free-stream layer is 3 cm. If we divide the velocity differential of 990 cm/s by the distance between the boundary layer and the free-stream layer, which is 3 cm, we end up with a velocity differential of 330 cm/s per centimeter. Looking at it a little bit closer: the velocity of the water would be 0 cm/s at the boundary; 330 cm/s at 1 cm from the boundary; 660 cm/s at 2 cm from the boundary, and 990 cm/s at 3 cm from the boundary. This incremental increase in speed per centimeter is known as the shear rate. To find the shear rate, we simply divide the speed of the free-stream velocity layer by the distance between the boundary layer and the free-stream velocity layer .
Viscosity
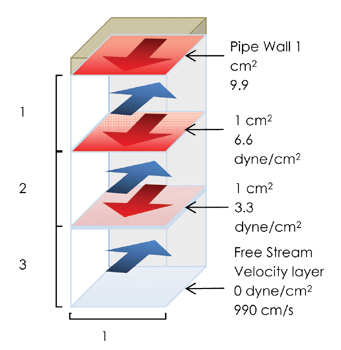
We understand so far that water moves in layers with one layer sliding over the other. Drag, or a force of friction, arises between the layers as they slide over one another. The force of friction is equal to the shear force that we have to apply to the water or to each layer to get it moving and keep it moving at whatever speed. This force, pushing against the inside surface of the pipe is equal to the shear force on each layer all added up. If we take the total shear force and divide it by the area of the inside wall of the pipe, we get the force acting on each square centimeter of the pipe, which is the shear stress at the pipe wall.
Imagine the inside wall of the pipe and the water moving through the pipe. Now imagine one square centimeter of the inside surface of the pipe. In your mind, color that one square centimeter red. Imagine that square centimeter becoming three dimensional, by extending it from the pipe wall to the center of the pipe. You now have a rectangle that is 1 cm x 1 cm x 3cm in your mind. The top of the rectangle is red and it is touching the inside wall of the pipe. The red color extends from one end of the rectangle to the other, but getting lighter and lighter until it fades completely at the end of the rectangle that is at the centre of the pipe.
The force at the top of the rectangle (the pipe wall) is 9.9 dyne. The velocity of the fluid at the top of the rectangle is 0 cm/s, and the velocity of the fluid at the bottom of the rectangle (the centre of the pipe) is 990 cm/s. The velocity differential, or the difference in speed from the top of the rectangle to the bottom of the rectangle is 990 cm/s. The force of 9.9 dyne, acting at the top of the rectangle is distributed evenly throughout the length of the rectangle, and so is the velocity differential. The total force of 9.9 dyne is the force required to create the total velocity differential of 990 cm/s. If we divide the force of 9.9 dyne by the length of the rectangle, we end up with the force required to create the velocity differential across 1 cm of the rectangle.
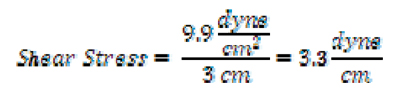
In our discussion above, we figured out that the shear rate was the velocity differential across 1 cm. In our example, the shear rate was 330 cm/s. The force of 3.3 dyne, which is the force we just calculated, is the force distributed across 1 cm, while the shear rate of 330 cm/s is the velocity differential across the same centimetre. The shear force of 3.3 dyne is the force required to create a velocity differential of 330 cm/s. If we go a step further, and we divide the force of 3.3 dyne by the velocity differential of 330 cm/s, we end up with the force required to create a velocity differential of 1 cm/s across the same centimetre. And this is what viscosity is: the force needed to create a velocity differential of 1 cm/s across 1 cm of fluid.
The basic formula for viscosity is:
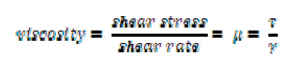
If we take the shear stress and shear rate values from our example, and plug them into the basic formula for viscosity, the result that we get is pretty interesting.
The result of the viscosity calculation shows that the viscosity of water is 1 centipoise, which means that it takes 0.01 dyne to create a velocity differential of 1 cm/s across 1 cubic centimeter of water. If we had a fluid that had a viscosity of 5 centipoise, then it would take 0.05 dyne to create a velocity differential of 1 cm/s across 1 cubic centimeter of fluid. If the viscosity was 100 centipoise, then it would take 1 dyne to create a velocity differential of 1 cm/s. The viscosity of a fluid refers to the force that it takes to create a velocity differential of 1 cm/s across 1 cubic centimeter of fluid .
Viscosity describes thickness in terms of the force that it takes to create a velocity differential of 1 cm/s across 1 cubic centimeter of fluid. Viscosity is about the relationship between force and the velocity differential that is created by that force. So viscosity describes thickness in terms of the force/velocity differential relationship. The processes that we typically use, which seem adequate given our intuitive understanding of thickness, tell us very little about the relationship between force and the resulting velocity differential. And as a result, they tell us very little about suspension and carrying capacity as these are a function of that relationship. In order to gain insight into the force/velocity differential relationship, we need to use alternative processes and have a level of understanding that is sufficient to interpret the outcome of those processes. There is an obvious and significant gap between the insight that our current processes afford, and the insight that we might gain using processes that are more commensurate with the nature of viscosity.
Manley Osbak is vice president of technical services at The Crossing Co., based in Nisku, Alberta, Canada.
